All You Need to Know About the Circumcenter of a Triangle

What is the Circumcenter of a Triangle?

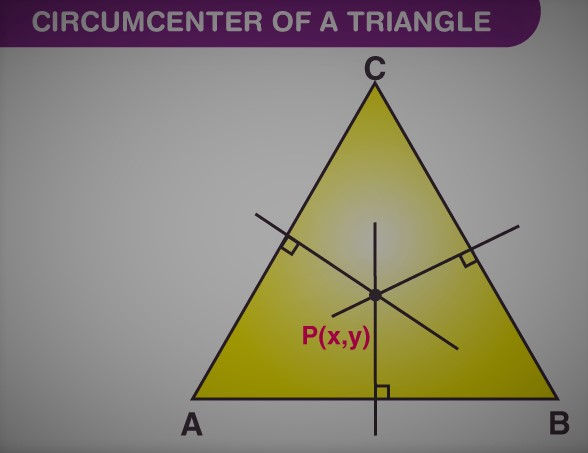
The circumcenter of a triangle is characterized as where the opposite bisectors of the sides of that specific triangle converge. As such, the purpose of the simultaneousness of the bisector of the sides of a triangle is known as the circumcenter. It is indicated by P(X, Y). The circumcenter is likewise the focal point of the circumcircle of that triangle and it tends to be either inside or outside the triangle.

Circumcenter Formula

P(X, Y) = [(x1 sin 2A + x2 sin 2B + x3 sin 2C)/(sin 2A + sin 2B + sin 2C), (y1 sin 2A + y2 sin 2B + y3 sin 2C)/(sin 2A + sin 2B + sin 2C)]

Here,

A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of the triangle and A, B, C are their individual points.

Technique to Calculate the Circumcenter of a Triangle

• Steps to discover the circumcenter of a triangle are:

• Ascertain the midpoint of given directions, for example midpoints of AB, AC, and BC

• Ascertain the slant of the specific line

• By utilizing the midpoint and the slant, discover the condition of the line (y-y1) = m (x-x1)

• Discover the condition of the other line along these lines

• Unravel two bisector conditions by discovering the convergence point

• The determined convergence point will be the circumcenter of the given triangle

• Discovering Circumcenter Using Linear Equations

The circumcenter can likewise be determined by framing straight conditions utilizing the separation recipe. Allow us to take (X, Y) be the directions of the circumcenter. As per the circumcenter properties, the separation of (X, Y) from every vertex of a triangle would be the equivalent.

Accept that D1 be the separation between the vertex (x1, y1) and the circumcenter (X, Y), at that point the recipe is given by,

D1= √[(X−x1)2+(Y−y1)2]

D2= √[(X−x2)2+(Y−y2)2]

D3= √[(X−x3)2+(Y−y3)2]

Presently, since D1=D2 and D2=D3, we get

(X−x1)2 + (Y−y1)2 = (X−x2)2 + (Y−y2)2

From this, two direct conditions are acquired. By fathoming the direct conditions utilizing replacement or disposal techniques, the directions of the circumcenter can be acquired.

Properties of Circumcenter

A portion of the properties of a triangle's circumcenter are as per the following:

• The circumcenter is the focal point of the circumcircle

• All the vertices of a triangle are equidistant from the circumcenter

• In an intense calculated triangle, the circumcenter lies inside the triangle

• In a harsh calculated triangle, it lies outside of the triangle

Circumcenter lies at the midpoint of the hypotenuse side of a right-calculated triangle

How to Find the Circumcenter of a Triangle?

To discover the circumcenter of any triangle, draw the opposite bisectors of the sides and expand them. Where the opposite crosses each other will be the circumcenter of that triangle.