How to Find the Circumcenter of a Triangle

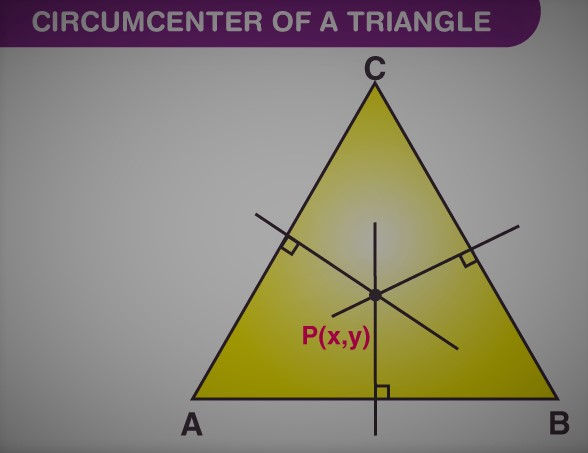
The purpose of the simultaneousness of the opposite bisectors of the sides of a triangle is known as the circumcenter of the triangle.

Stage 1 :

Discover the conditions of the opposite bisectors of any different sides of the triangle.

Stage 2 :

Explain the two conditions found in sync 2 for x and y.

The arrangement (x, y) is the circumcenter of the triangle given.

Example :

Discover the coordinates of the circumcenter of a triangle whose vertices are (2, - 3), (8, - 2), and (8, 6).

Also Read: https://officalad007.wixsite.com/classical-physics/post/easiest-way-to-calculate-the-circumcenter-of-a-triangle

Solution :

Let A(2, - 3), B(8, - 2), and C(8, 6) be the vertices of the triangle.

D is the midpoint of AB and E is the midpoint of BC.

The midpoint of AB is

= [(x1 + x2)/2, (y1 + y2)/2]

Substitute (x1, y1) = (2, - 3) and (x2, y2) = (8, - 2).

= [(2 + 8)/2, (- 3 - 2)/2]

= [10/2, - 5/2]

= (5, - 5/2)

Thus, the point D is (5, - 5/2).

The slant of AB is

= [(y2 - y1)/(x2 - x1)]

Substitute (x1, y1) = (2, - 3) and (x2, y2) = (8, - 2).

= [(- 2 - (- 3)]/(8 - 2)

= (- 2 + 3)/6

= 1/6

The slant of the opposite line to AB is

= - 1/slant of AB

= - 1/(1/6)

= - 1 ⋅ (6/1)

= - 6

Condition of the opposite bisector to the side AB :

y = mx + b

Substitute m = - 6.

y = - 6x + b - (1)

Substitute the point D(5, - 5/2) for (x, y) into the above condition.

- 5/2 = - 6(5) + b

- 2.5 = - 30 + b

Add 30 to each side.

27.5 = b

Substitute b = 27.5 in (1).

(1)- - > y = - 6x + 27.5

Condition of the opposite line through D is

y = - 6x + 27.5 - (2)

The midpoint of BC is

= [(x1 + x2)/2, (y1 + y2)/2]

Substitute (x1, y1) = (8, - 2) and (x2, y2) = (8, 6).

= [(8 + 8)/2, (- 2 + 6)/2]

= [16/2, 4/2]

= (8, 2)

Thus, the point E is (8, 2).

The incline of BC is

= [(y2 - y1)/(x2 - x1)]

Substitute (x1, y1) = (8, - 2) and (x2, y2) = (8, 6).

= [6 - (- 2)]/(8 - 8)

= (6 + 2)/0

= 8/0

Incline of the opposite line to BC is

= - 1/incline of BC

= - 1/(8/0)

= - 1 ⋅ (0/8)

= - 1 ⋅ 0

= 0

Condition of the opposite bisector to the side BC :

y = mx + b

Substitute m = 0.

y = b - (3)

Substitute the point E(8, 2) for (x, y) into the above condition.

2 = b

Substitute b = 2 in (1).

(1)- - > y = 2

Condition of the opposite line through D is

y = 2 - (4)

Explaining (2) and (4), we get

x = 4.25 and y = 2

Along these lines, the circumcenter of the triangle ABC is

(4.25, 2)

The upper procedure will be valuable in how to find the circumcenter of a triangle.